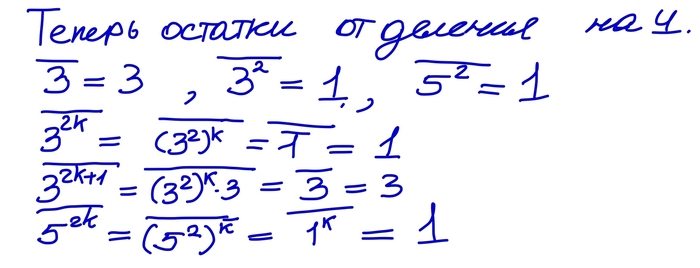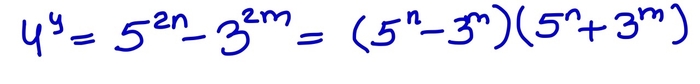Теорема эта утверждает вот что -- если дана сфера, то её можно разрезать на несколько (конечное число!) частей, передвинуть эти части и получить в итоге две ровно такие же сферы. Дальше, с помощью этого можно доказать, что тоже самое верно для шара, куба, в общем почти чего угодно -- это обсудим в конце. В частности, например, из того же апельсина вы можете собрать Юпитер : )
Звучит абсурдно? Конечно! Но, давайте посмотрим, почему это всё-таки можно сделать.
Ворнинг 1: я буду много где использовать понятие множества и в некоторых местах использовать понятия счётной бесконечности и континуума. Про это всё я уже писал несколько постов, кто не знает что это такое, но кому интересно -- вот ссылки:
Множества и их парадоксы
Бесконечный рассказ о бесконечности. Часть первая
Бесконечный рассказ о бесконечности. Часть вторая
Ворнинг 2: поскольку всё же мы с вами будем доказывать вполне себе серьёзную теорему, мне придётся делать некоторое количество математических выкладок. Чтобы это не превратилось в абстрактный кошмар, я буду делать много картинок и пытаться объяснять суть. Из-за этого пост получился достаточно большим, так что рекомендую делать перерывы).
Также, для того чтобы вы всегда видели свет в конце туннеля и понимали "ну сколько ещё это можно читать", я сразу разделю пост на части и приведу тут содержание. Так, надеюсь, вам будет проще ориентироваться.
Содержание:
Часть 1. Терминология и постановка задачи
Часть 2. "Бесполезная" лемма (лемма о промежуточных множествах)
Часть 3. Начало доказательства теоремы, основная конструкция
Часть 4. Раскрашиваем сферу
Часть 5. Завершение доказательства (тут будет наибольшее количество формул, но все они будут проиллюстрированы)
Часть 6. Что пошло не так?
Бонус: доказательство вспомогательного утверждения (для тех, кому интересно как используется тот факт, что континуум больше чем счётная бесконечность).
Итак, начнём!
Часть 1. Терминология и постановка задачи.
Допустим, есть у нас обыкновенное трёхмерное пространство и в нём два множества -- X и Y. Мы будем их называть изометричными, если существует такое движение пространства, что X переходит в Y. Иначе говоря, мы можем с помощью параллельных переносов и поворотов в пространстве перенести одно множество в другое. Можно к этому определению ещё добавить симметрии, но нам они не понадобятся.
Теперь, допустим даны какие-то другие множества X и Y. Я буду говорить что они равносоставлены, если существуют разбиение X на конечное число взаимно непересекающихся подмножеств X₁,...,Xₖ и аналогичное разбиение Y на Y₁,...,Yₖ (число частей одинаковое!), что для каждого i=1,...,k верно, что Xᵢ изометрично Yᵢ.
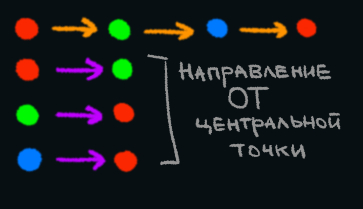
Короче говоря, это просто формализация той идеи, которую я высказал раньше -- множества равносоставлены, если можно порезать их на одинаковое число кусков, так, чтобы эти куски были попарно "одинаковы". Вот вам картинка для понимания этих терминов в плоском случае:
(Треугольник X₂ берется без диагонали, поэтому у нас остаётся кусочек отсутствующей границы)
Я буду писать X ~ Y, если X равносоставлен с Y. Вот несколько свойств равносоставленности:
1. X ~ X для любого множества X (очевидно)
2. Если X ~ Y, то Y ~ X (симметрично -- тоже очевидно, просто поверните процесс в обратном порядке).
3. Если X ~ Y и Y ~ Z, то X ~ Y (это свойство называется транзитивность. Сравните с равенством -- x = y, y = z => x = z). Это свойство чуть менее очевидно, но попробуйте доказать это как упражнение -- тут важно, что количество частей на которое надо разбить X чтобы собрать Z будет больше, чем для того чтобы просто собрать Y.
4. Если X и Y изометричны, то они равносоставлены (совсем очевидно, зато из этого следует, что свойства 1-3 верны и для изометричности).
Теперь наконец-то мы можем сформулировать теорему, которую собираемся доказывать:
Теорема. Двумерная сфера равносоставлена с двумя своими копиями.
На математическом языке это можно сформулировать так: S ~ S⊔S. Символ ⊔ обозначает так называемое дизъюнктное объединение, т.е. мы по сути берем копию сферы и относим её куда подальше, чтобы она не пересекалась с изначальной. Я так же буду использовать этот символ когда хочу показать что множество состоит из не пересекающихся частей.
Теорема выглядит абсурдно -- как вообще может быть такое, что мы разобрали поверхность какой-то площади, а собрали из тех же частей поверхность вдвое большей площади? Но тем не менее это сделать можно и мы скоро увидим как.
Часть 2. "Бесполезная" лемма (лемма о промежуточных множествах)
Прежде чем доказывать теорему, мы докажем, на первый взгляд, бессмысленную лемму: Допустим, что есть множество A, его подмножество B и в нём еще одно подмножество A₁, т.е. A ⊃ B ⊃ A₁. И предположим, что самое большое множество оказалось равносоставлено с самыми меньшим -- A ~ A₁. Тогда все три множества равносоставлены -- A ~ B ~ A₁. Вот коротка формулировка:
Лемма: A ⊃ B ⊃ A₁, A ~ A₁ => A ~ B ~ A₁
Почему эта лемма выглядит бессмысленной? Да потому что, казалось бы, изначально такой ситуации не может быть -- действительно, как может случиться такое, "большое" множество порезали на части, просто так их подвигали и получили "маленькое" (в смысле, например объёма). С другой стороны, мы собираемся доказывать нечто похожее, так что давайте предположим, что всё-таки такая ситуация может случиться.
Итак, доказательство:
Предположим, что такое преобразование существует: у нас есть функция f:A -> A₁, которая реализует нашу операцию разрезания на части А и последующей сборки A₁. Т.е. каждая точка а∈А посредством действий, которые мы зашифровали как f переходит в какую-то точку f(a) ∈ A₁. А что произойдет если изначально эта точка уже была в A₁? Выйти за пределы A₁ оно не может. Значит если взять все точки множества A₁ и подействовать нашим преобразованием f, мы получим некоторое подмножество A₂ ⊂ A₁ (коротко -- f(A₁) = A₂ ⊂ A₁). Заметим, что раз f изначально делило на части A и собирало A₁, то, очевидно, оно так же будет делить A₁ и собирать A₂ (действительно, разрезав большее множество на части мы так же разрежем и меньшее подмножество, может быть на меньшее число частей). Значит A₁ ~ A₂. Аналогично мы можем продолжить эту конструкцию -- множество A₂ при f перейдёт в какое-то подмножество себя, которое мы назовём A₃:
f(A₂) = A₃ ⊂ A₂. Аналогично мы получили A₃ ~ A₂. И так далее -- будем строить такую бесконечную цепочку f(Аₖ) = Аₖ₊₁ ⊂ Аₖ и Аₖ₊₁ ~ Аₖ.
А что происходит с "промежуточным" множеством B? Аналогично первому случаю, мы будем получать бесконечную цепочку множеств f(Bₖ) = Bₖ₊₁ ⊂ Aₖ₊₁ ⊂ Bₖ. Точно так же как и предыдущем варианте, Bₖ₊₁ ~ Bₖ, т.е. они равносоставлены!
В итоге у нас есть такая вот бесконечная цепочка вложенных подмножеств:
A⊃ B⊃ A₁⊃ B₁⊃ A₂⊃ B₂⊃ ...⊃ Аₖ⊃ Bₖ⊃ Аₖ₊₁⊃ Bₖ₊₁⊃ ...
Эта цепочка уменьшающихся множеств, но "в пределе" может получиться что-то не пустое -- давайте обозначим пересечение всех этих множеств за С. Для тех, кто уже запутался, вот вам картинка:
Тут исходное множество А -- это весь большой прямоугольник (и все точки внутри него). B -- всё точки внутри самого большого эллипса. Множество A₁ -- следующий прямоугольник. И так далее. Множество С -- это то множество, где f его не уменьшает, т.е. оставляет таким же -- f(C) = C. При этом точки внутри С могут двигаться при действии f, т.е. они не фиксированы, просто на их место всегда придут снова точки из С.
Давайте теперь раскрасим эту картинку -- все кусочки, которые внутри прямоугольников, но вне овалов покрасим в оранжевый, а все остальные, т.е. те, которые внутри овалов, но вне прямоугольников -- в зелёный. Формульно это выглядит так --
"оранжевое множество" = A\B ⊔ A₁\B₁ ⊔ ... ⊔ Аₖ\Bₖ ⊔ ...
''зелёное множество" = B\A₁ ⊔ B₁\A₂ ⊔ ...⊔ Bₖ\Аₖ₊₁ ⊔ ...
(тем, кто не знаком с математикой: символ "\" -- это разность множеств, т.е. A\B это те точки A, которые не в B.).
Синим закрасим точки из С.
Заметим, что при действии f оранжевое множество переходит почти само в себя, а именно оно "углубляется само в себя на один слой":
f(A\B ⊔ A₁\B₁ ⊔ ... ⊔ Аₖ\Bₖ ⊔ ...) = A₁\B₁ ⊔ ... ⊔ Аₖ\Bₖ ⊔ ...
Более того, оно таким образом равносоставлено с собой без внешнего слоя -- действительно, f изначально резало всё на конечное число частей, значит и оранжевое множество порежется на то же число частей и соберёт само себя.
И вот, финальный шаг -- разрежем наше множество на 2 части -- рыжую и (зеленую + синюю). Рыжую часть мы пересоберём посредством f. Оставшуюся часть мы просто оставим на месте, даже резать не будем! Что получится в итоге? Получится самый большой овал, т.е. множество B!
Вот вам ещё картинка где, надеюсь, более наглядно объяснено что происходит:
(id -- тождественное отображение, т.е. то, которое ничего не делает с точками). Белые линии используются исключительно для разделения, представьте себе что их нет.
Ура, мы доказали "бесполезное" утверждение -- теперь если мы знаем, что множество равносоставлено со своим подмножеством, то и все промежуточные подмножества мы умеем собирать из большого (следовательно и из маленького).
Пришло время переходить к доказательству нашей теоремы о том, что сфера равносоставлена с двумя своими копиями.
Часть 3. Начало доказательства теоремы, основная конструкция
Проведём через центр сферы две прямые -- рыжую и фиолетовую. Зададим два действия:
1. Поворот сферы вокруг рыжей прямой на угол 120° ("рыжий поворот"), мы обозначим его буквой α.
2. Поворот сферы вокруг фиолетовой прямой на угол 180° ("фиолетовый поворот"), это действие мы обозначим буквой β.
Будем рассматривать всевозможные комбинации таких поворотов, скажем αβααβ это сначала "рыжий" поворот, потом "фиолетовый", потом два "рыжих" и потом снова "фиолетовый". Очевидно так же, что ααα это просто тождественное отображение -- действительно, три раза повернуть на 120° это тоже самое что ничего не делать. Аналогично ββ -- тождественное отображение.
Первый вопрос, который нам нужно решить такой -- допустим мы сделали некоторую последовательность рыжих и фиолетовых поворотов, причем так, чтобы не было нигде трёх рыжих подряд или двух фиолетовых. Может ли быть такое, что в результате получилось тождественное отображение? (т.е. какое-нибудь длинное слово вида β..αβα внезапно ничего не делает со сферой). Такое может случиться, если мы неправильно подобрали угол между прямыми (например если две прямые совпадают, преобразование αβ будет просто поворотом на 60° градусов, поэтому αβαβαβαβαβαβ даст тождественное преобразование. Но можно ли подобрать угол между прямыми такой, что такой ситуации никогда не возникнет? Оказывается, да, можно! Я не буду сейчас доказывать, скажу лишь то, что "плохих" углов у нас достаточно мало, "всего лишь" счетное число, а возможных выборов у нас целый континуум. Для строгого доказательства требуется погрузиться в тригонометрию, что конечно же сейчас делать совершенно не нужно.
Отлично, теперь мы знаем, что теперь никакая комбинация поворотов у нас не будет давать тривиальное преобразование. Это, кстати, равносильно тому, что никакие две различные комбинации поворотов не будут давать одинаковое преобразование.
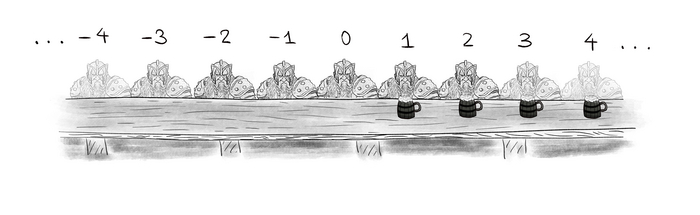
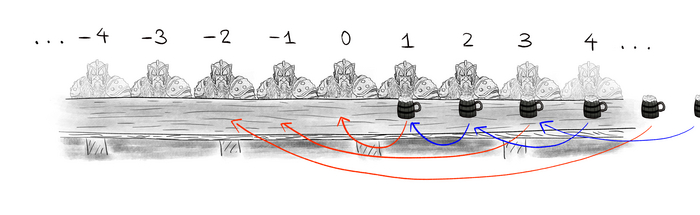
Давайте теперь возьмём точку на сфере (не лежащую на осях). Будем над ней совершать всевозможные разрешенные повороты и каждый раз оставлять "след", т.е. смотреть на те точки сферы, куда она может прибежать. Начало пути будет выглядеть примерно так:
Тут мы начинаем с точки Е и проделываем с ней всевозможные действия, которые можно придумать. Например, А=α(Е), АА=αα(Е), BAAB=βααβ(E) и т.д. Почему на рисунке они раскрашены в разные цвета я обсужу позже, пока это не важно.
Для каждой точки мы таким образом можем построить её орбиту -- т.е. множество точек, которое мы можем получить в результате комбинации рыжих и фиолетовых поворотов.
Посмотрим на эти орбиты повнимательнее. Во-первых очевидно каждая точка принадлежит какой-то орбите -- например той, которую она сама порождает. Во-вторых, если вдруг оказалось, что две каких-то орбиты пересекаются, то на самом деле они совпадают (проверьте сами, отличное упражнение на логику и понимание происходящего)!
Как итог -- вся сфера разбивается на очень очень много таких орбит.
Теперь рассмотрим любую точку. Назовём её "плохой", если существует какая-то последовательность поворотов, которая приводит эту точку в саму себя. Например точка лежащая на любой из осей -- "плохая". Остальные точки будут назовем "хорошими". Опять же очевидно, что если точка "плохая", тогда и любая точка из её орбиты "плохая". Тоже самое верно про "хорошие" -- для "хороших" точек все ее возможные положения тоже "хорошие".
Сколько плохих точек у нас есть? На самом деле это не так сложно понять -- любая плохая точка принадлежит орбите точки пересечения одной из осей со сферой. Т.е. суммарно у нас всего четыре таких орбиты, каждая из них содержит всего счётное число точек (потому что любая последовательность поворотов однозначно задаётся конечным словом из букв α и β, а таких слов счётно). Итого, "плохих" точек у нас счётное число!
Что у нас на текущий момент есть? Вся сфера разбита на орбиты -- каждая орбита есть множество точек, где от любой можно добраться до любой с помощью наших поворотов. Из них у нас есть четыре "плохих" орбиты, но, к счастью, это даёт счётное число "плохих" точек (почему это важно выяснится чуть позже). Что теперь? Надо раскрасить эти точки!
Часть 4. Раскрашиваем сферу
Давайте возьмём произвольную хорошую орбиту и возьмём в ней произвольную точку, которую назовём стартовой. Покрасим её в красный цвет. Далее будем раскрашивать точки итеративно по следующему правилу: допустим мы покрасили очередную точку а и нам надо покрасить следующую (т.е. полученную одним из двух поворотов), ещё не покрашенную, точку b. Делать это будем по следующему правилу:
1. Если а красная и b получена рыжим поворотом -- красим b в зелёный.
2. Если а зелёная и b получена рыжим поворотом -- красим b в синий.
3. Если а синяя и b получена рыжим поворотом -- красим b в красный.
4. Если а красная и b получена фиолетовым поворотом -- красим b в зелёный.
5. Если а зелёная или синяя и b получена фиолетовым поворотом -- красим b в красный.
Вот правило раскраски в картинках.
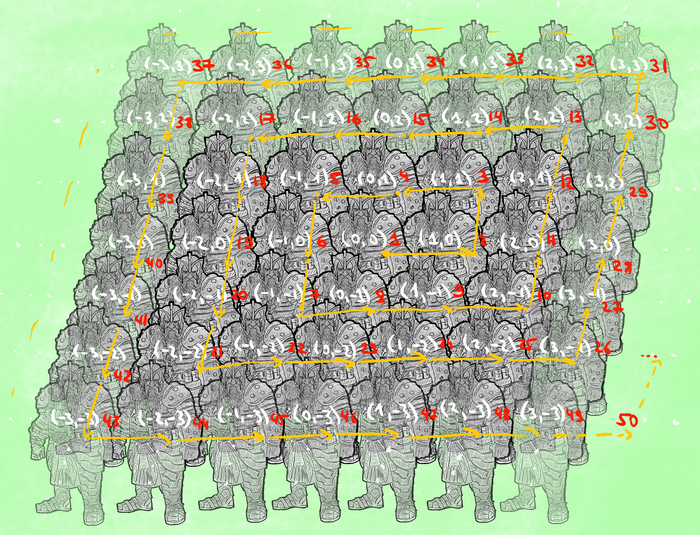
Выглядеть наша хорошая орбита будет примерно так:
Картинка, ради которой делался пост : )
Для не указываю направление, потому что ββ это тождественное отображение.
Заметьте, что эта гирлянда не симметрична -- очень важно где именно находится начальная точка.
Буквы кодируют каждую точку орбиты -- А соответствует рыжему повороту, B -- фиолетовому.
Теперь происходит магия -- мы неожиданно замечаем, что:
Если повернуть ВСЕ красные точки на рыжий поворот, то получатся ВСЕ зелёные точки.
Если повернуть ВСЕ зелёные точки на рыжий поворот, то получатся ВСЕ синие точки.
Если повернуть ВСЕ синие точки на рыжий поворот, то получатся ВСЕ красные точки.
Если повернуть ВСЕ красные точки на фиолетовый поворот, то, (магия), получатся ВСЕ синие и зелёные точки, т.е. вообще все оставшиеся!
Итак, что мы сделали? Мы раскрасили все точки сферы в четыре цвета -- плохие в серый, хорошие в красный, зелёный и синий. Хорошие точки мы красили по следующему принципу -- выбирали в каждой орбите по начальной точке, и красили все остальные точки в ней по определённому правилу. Получилось в итоге три множества -- красное, зелёное и синее. Давайте их обозначим R, G, B (буква B уже была в обозначениях точек, но это нигде не пригодится больше, так что будем использовать тут).
Мы выяснили, что с помощью рыжего поворота красное множество переводится в зелёное, зелёное в синее, синее в красное. Значит, все три множества равносоставлены:
R ~ G ~ B ~ R.
Так же мы выяснили, что с помощью фиолетового поворота, красное множество переходит в объединение зелёного и синего:
R ~ G ⊔ B.
Наблюдение из этого всего:
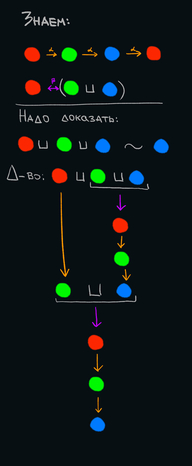
Все множество хороших точек R ⊔ G ⊔ B равносоставлено с B. Доказательство:
Мы знаем, что G ⊔ B ~ R, а R ~ B. Значит R ⊔ (G ⊔ B) ~ B ⊔ R ~ B ⊔ G ~ R ~ B. Вот картинка, которая поясняет это доказательство:
Часть 5. Завершение доказательства
Для того, чтобы всё окончательно получилось, нам нужно разобраться с "плохим" множеством серых точек (давайте назовём его Ξ (большая буква "Кси")). Мы помним, что оно счётно. Я утверждаю, что существует некоторый поворот φ (не рыжий или фиолетовый, вокруг вообще другой оси может быть), такой, что если Ξ повернуть c помощью φ, то полученное множество φ(Ξ) станет полностью "хорошим", т.е. Ξ не будет пересекаться с φ(Ξ).
Почему это так? В этот раз я таки докажу это строго, но в самом конце поста, чтобы мы не тянули с доказательством теоремы.
Итак, у нас есть поворот , такой, что φ(Ξ) -- подмножество R ⊔ G ⊔ B. Мы уже доказали, что R ⊔ G ⊔ B равносоставлено с B, значит и φ(Ξ) равносоставлено с некоторым подмножеством B. Обозначим это подмножество как Ѯ (видимо это тоже большая Кси...).
Наша сфера представима теперь двумя способами: S = Ξ⊔R⊔ G⊔ B и S = (Ξ ⊔ R) ⊔ (Ѯ G) ⊔ (B \ Ѯ). Во втором случае мы разбили сферу на три части: Ξ ⊔ R, Ѯ ⊔ G (добавили к всем зеленым часть синих) и B \ Ѯ (все что осталось). Теперь, наконец-то получаем вот что:
1. Ξ ⊔ R ~ Ξ ⊔ B ⊔ G ~ Ξ ⊔ R ⊔ B ~ Ξ ⊔ B ⊔ G ⊔ R ~ S
2. Ѯ ⊔ G ~ Ξ ⊔ R ~ ... ~ S
Что мы получили? Мы получили, что наша сфера вот в представлении S = (Ξ ⊔ R) ⊔ (Ѯ G) ⊔ (B \ Ѯ) собирается в две сферы + какой-то небольшой остаток (B \ Ѯ): S ~ S ⊔ S ⊔ (B \ Ѯ). Но мы же с вами доказывали в самом начале лемму, которая как раз здесь очень хорошо может пригодиться: у нас есть большое множество S ⊔ S ⊔ (B \ Ѯ) и маленькое, равносоставленное ему множество S. Нам нужно получить всё, что в середине, т.е. множество S ⊔ S. И лемма утверждает, что мы можем это сделать!
Теорема доказана.
Вот картинка, которая демонстрирует доказательство:
Поздравляю тех, кто добрался до этого момента!
Что даёт нам эта теорема? Например, она даёт точно таким же образом доказать её аналог для "апельсинов" -- любой шар равносоставлен двум своим копиям. Делается это очень просто -- шар у нас состоит из кучи сфер + центральная точка. Все сферы одновременно мы преобразовываем в две своих копии, а с центральной точкой мы разбираемся при помощи леммы о промежуточном множестве.
Мало того, эта лемма позволяет доказать ещё одно утверждение -- допустим есть (сколь угодно) маленький шар и (тоже сколь угодно) большой шар. Тогда они равносоставлены. Доказывается это так -- разрежем большой шар на много-много маленьких частей, таких что каждую из них можно поместить в маленький шар. Теперь продублируем маленький шар столько раз, сколько частей. А дальше используем нашу лемму о промежуточном множестве! Получается вы из горошины сможете собрать, например, наше Солнце).
Часть 6. Что пошло не так?
Мы получили что-то, что противоречит здравому смыслу. Казалось бы всю теорию множеств можно выкидывать на свалку после таких результатов -- как вообще нечто такое может описывать что-то реальное? И примерно такая реакция и была у математиков, когда был получен этот результат. Но вот вопрос, почему мы сумели вообще сделать такое?
На самом деле, все шаги в нашем доказательстве были абсолютно интуитивно понятные и не нарушающие законы мироздания, кроме одного. Помните момент, в котором мы в каждой орбите выбрали по "стартовой" точке? Казалось бы, каждая орбита есть множество не пустое, так кто мешает выбрать в каждой по точке? Вот на самом деле именно тут зарыта проблема -- этих орбит бесконечно много. Поэтому вам никто никогда не скажет КАК выбрать начальные точки. Т.е. не существует никакого алгоритма, формулы и т.д., которое позволило бы сказать -- а вот в этой вот орбите мы возьмём вот эту вот точку в качестве старта. Оказывается, существование такого выбора невозможно просто так доказать, это некоторая самостоятельная аксиома теории множеств, которая так и называется -- аксиома выбора.
Насчёт неё я однажды напишу отдельный пост, потому что оказывается, что именно она позволяет делать вот такие вот ужасные конструкции.
В частности, заметим, что мы только что доказали с помощью неё, что для некоторых множеств в пространстве невозможно определить понятие объёма. Действительно, если бы каждое множество имело объём, то мы не могли бы провести эту процедуру сборки из маленького шара огромного -- каждая часть имела бы объём и сумма объёмом частей была бы постоянной. В данном же случае те части, на которые мы делим шар объём вообще иметь не будут! Это отличная затравка для следующей возможной темы -- а что вообще тогда такое объём множества?
А вообще, всё-таки реальные объекты состоят не из точек, а всё же из частиц. Так что к сожалению с апельсинами наша стратегия не сработает(
Вот такие вот дела, мы выяснили что с математикой надо быть осторожнее. Всем, кто сумел осилить это всё -- большое спасибо! А для тех кто ещё и не умер -- маленький бонус в конце.
Бонус: доказательство вспомогательного утверждения
Теперь я приведу очень изящное, на мой взгляд, доказательство того факта, который я обещал доказать строго.
Утверждение: пусть Ξ -- любое счётное подмножество сферы. Тогда существует поворот φ, такой, что φ(Ξ) не пересекается с Ξ.
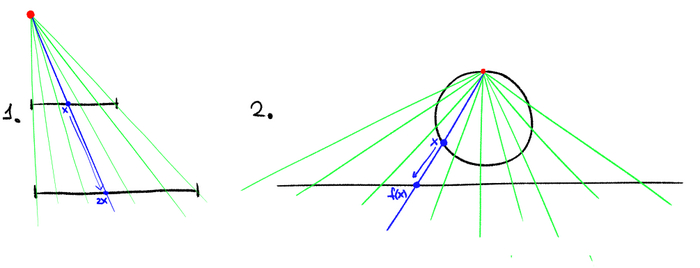
Доказательство: для начала рассмотрим две произвольные точки сферы -- a и b. Допустим, что при каком-то повороте относительно какой-то оси а перешло в b. Легко видеть, что эта ось может проходить только лишь через, так называемый большой (т.е. тот, который делит сферу на две равные половинки) круг, проходящий между a и b.
Теперь, допустим, что при каком-то повороте Ξ пересекается со своим образом. Значит есть точки а и b из такие, что а переходит в b. Значит ось должна была проходить через большой круг, проходящий между а и b. Но таких пар а и b счётное число, значит и таких больших кругов может быть счётное число. Значит если какая-то ось не пересекает ни один из них, то любой поворот вокруг нее будет таким, каким нам нужно! Осталось доказать, что существует точка вне этого счётного семейства кругов. Тут возникает типичный приём связанный с мощностями множеств: всего на сфере у нас есть континуум больших кругов. Значит существует такой круг, что он не принадлежит нашему семейству. При этом, он пересекает каждый круг из семейства ровно в двух точках, значит точек пересечения тоже счётно. Но при этом на самом круге континуум точек! Значит есть точка, которая не принадлежит никакому из больших кругов семейства! Ура, это то, что нам надо было доказать.