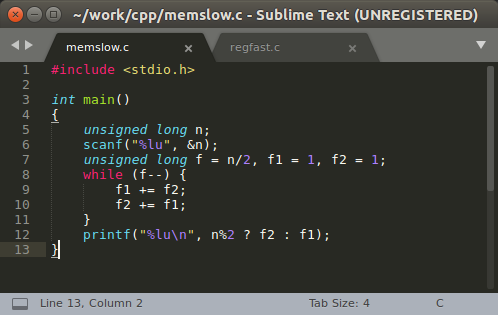
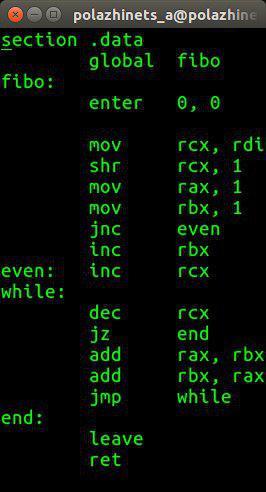
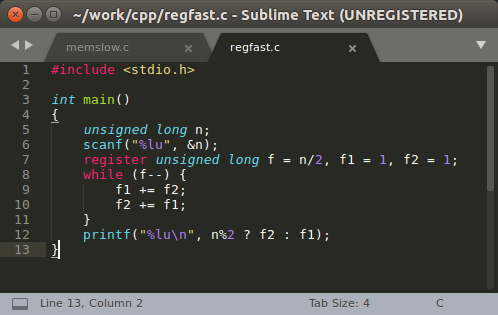
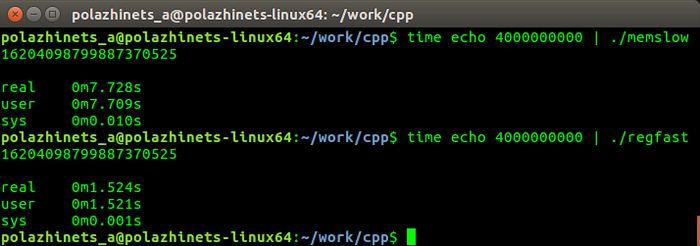
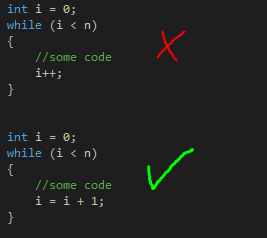
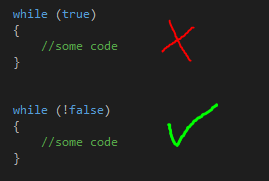
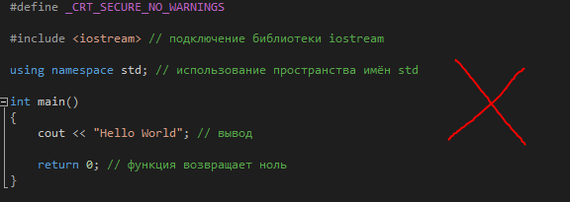
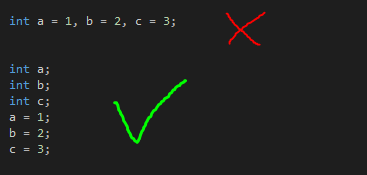Я не занимаюсь профессионально ни математикой, ни программированием (ABAP не считается), поэтому написанное ниже может показаться специалистам довольно банальным и очевидным, но я не исключаю, что кому-то из начинающих разработчиков приведенные в посте решения могут пригодиться.
Итак. Задача -- нарисовать в 3d поверхность, которая задана не набором полигонов, а формулой.
Алгоритм был выбран следующий:
0. Исходные данные.
*Координаты нулевой точки поверхности (точка в глобальной системе координат, являющаяся центром координат для формулы, которой задана поверхность);
*Вектор нормали поверхности в нулевой точке (показывает, как наклонена поверхность относительно глобальных координат);
*Размеры поверхности по x, y и z (чтобы она просчитывалась не по бесконечность во все стороны, а в рамках определенного объема);
*Координаты "глаза";
*Вектор направления взгляда;
*Вектор, показывающий, где у "глаза" верх;
1. Формируем лучи из каждого пикселя экрана и проверяем на пересечение с поверхностью.
2. Если луч не пересекается с поверхностью -- окрашиваем пиксель в черный.
3. Если пересекается -- определяем освещенность точки. Для этого определяем нормаль к поверхности плоскости, и чем меньше угол между нормалью и лучом из камеры -- тем ярче точка.
Давайте разбираться с каждой задачей в отдельности.
1. Лучи из каждого пикселя экрана.
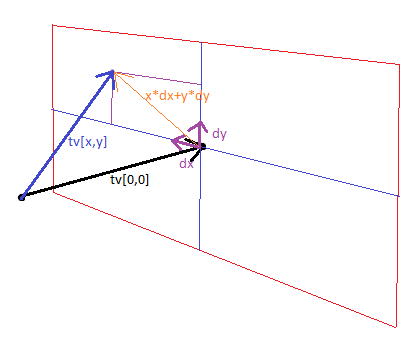
Ну, тут все просто. Чтобы задать луч -- нужна точка и вектор. Точка у нас есть -- это координаты "глаза". И направление взгляда есть. Соответственно, луч для координат [0,0] у нас уже есть. Что же делать с остальными координатами? Ответ на этот вопрос даст (или нет) эта картинка:
Для начала, нам нужны единичные векторы dx и dy, перпендикулярные друг другу и вектору взгляда, чтобы построить на них плоскую систему координат, которая будет для нас экраном. Вектор dy у нас уже есть («Вектор, показывающий, где у "глаза" верх» в исходных данных). Что же на счет dx? А тут приходит на помощь векторная алгебра, из которой мы помним (или нет), что результатом векторного произведения двух векторов является вектор, перпендикулярный векторам-множителям, с нормой равной площади параллелограмма, построенного на этих векторах. Соответственно, если исходные векторы перпендикулярны друг другу и оба с длиной равной единице – длина результата тоже будет равен единице. А это прекрасно, ведь нам нужен именно единичный вектор.
Таким образом,
dX[0] = tv[1]*dY[2] - tv[2]*dY[1];
dX[1] = tv[2]*dY[0] - tv[0]*dY[2];
dX[2] = tv[0]*dY[1] - tv[1]*dY[0];
где tv — вектор направления взгляда, а dY вектор, показывающий где у взгляда верх.
Дальше, было бы неплохо определиться с длиной векторов dx и dy, определив таким образом размер экрана (по сути, это управление углом обзора). Мне оптимальным показался вариант, когда у экрана размер равен единице
dX[0] /= max_x;
dX[1] /= max_x;
dX[2] /= max_x;
dY[0] /= max_x;
dY[1] /= max_x;
dY[2] /= max_x;
Где max_x – разрешение экрана по x. Да, dy тоже делится на max_x, чтобы длина вектора dx была равна вектору dy, так как иначе изображение будет растянуто по одной из осей.
Итак, у нас есть:
dX, dY – векторы, определяющие плоскость экрана.
dZ – вектор направления взгляда.
for (int y = 0; y <= max_y; ++y) {
for (int x = 0; x <= max_x; ++x) {
tv[0] = dZ[0]+x*dX[0]+y*dY[0];
tv[1] = dZ[1]+x*dX[1]+y*dY[1];
tv[2] = dZ[2]+x*dX[2]+y*dY[2];
// tv – вектор, показывающий направление луча из точки [x,y] экрана
// ...
};
};
В рамках этого цикла мы и будем работать дальше.
2. Пересечение луча с поверхностью.
Обычно лучший способ найти в пространстве точку пересечения луча с поверхностью, которая задана формулой – это решить систему уравнений, состоящую из уравнения плоскости и уравнения луча. Но если в уравнение плоскости проникает тригонометрия – решений становится бесконечное множество (буквально бесконечное, вида x = 0 ± 2πn, где n∈R ), и что делать программно с этой бесконечностью – не ясно. Поэтому мы будем искать точку пересечения итеративно:
1. Определяем параллелепипед, ограничивающий нашу поверхность (мы помним, что по условиям ограничили ее в размерах).
2. Ищем точки пересечения луча и параллелепипеда. Получаем 2 точки – «вход» и «выход» в пределы параллелепипеда.
3. В точке «входа» переводим координаты из глобальной системы координат в локальную для параллелепипеда.
4. В локальных x и у находим по формуле поверхности координату z. Если найденная координата z больше, чем у точки «входа», фиксируем, что мы «под» поверхностью. Иначе – фиксируем, что мы «над» поверхностью.
5. От точки «входа» до «выхода» проверяем аналогичным образом все точки на луче с заданным шагом. Как только на следующем шаге состояние отличается от того, что было на предыдущем – значит, нашли точку пересечения.
6. Если до точки «выхода» состояние не менялось – значит пересечения не было.
Теперь по пунктам.
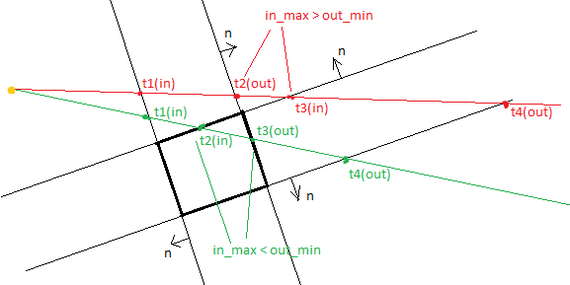
Существует простой и понятный алгоритм быстрого поиска пересечения прямоугольника с лучом на плоскости. Для его понимания нужно ввести пару терминов:
Точка входа – точка пересечения луча с прямой, в случае если нормаль этой прямой направлена навстречу лучу.
Точка выхода – точка пересечения луча с прямой, в случае если нормаль этой прямой направлена навстречу лучу.
Алгоритм такой:
Проверяем каждую прямую на пересечение с лучом и определяем для каждой точку входа или выхода. Если самая дальняя из найденных точек входа ближе, чем самая ближняя из найденных точек выхода, то это значит, что луч пересекает прямоугольник в этих точках. Если самая дальняя из найденных точек входа дальше, чем самая ближняя из найденных точек выхода, то это значит, что луч не пересекает прямоугольник.
К чему это я? А вот к чему. Этот подход отлично работает и в пространстве, если заменить 4 прямые на 6 плоскостей.
Как мы помним, поверхность задана точкой и нормалью и ограничена в размерах по x, y и z. Причем эти x y и z – в локальных координатах. То есть наш параллелепипед, ограничивающий поверхность, должен уметь вращаться вместе с поверхностью.
Поэтому для начала определим эти плоскости с учетом поворота параллелепипеда с поверхностью. Для этого нам понадобятся 3 вектора:
ddX[3] = {0,0,0}; // единичный вектор, который направлен вдоль оси X нашей поверхности
ddY[3] = {0,0,0}; // единичный вектор, который направлен вдоль оси Y нашей поверхности
ddZ[3] = {0,0,0}; // единичный вектор, который направлен вдоль оси Z нашей поверхности
с ddZ все понятно – это нормаль к поверхности.
С ddX и ddY сложнее. Одной только точкой и нормалью можно задать в пространстве только бесконечную поверхность. А тут нам нужно зафиксировать поворот этой плоскости вокруг оси z. Это можно сделать разными способами – я беру еще одну точку на плоскости и фиксирую ее координаты в глобальной системе координат. Допустим, это точка point2, а нулевая точка поверхности — point. Тогда
ddX[0] = point2[0] - point[0];
ddX[1] = point2[1] - point[1];
ddX[2] = point2[2] - point[2];
len = sqrt(ddX[0]*ddX[0]+ddX[1]*ddX[1]+ddX[2] *ddX[2]) ;
ddX[0]/=len;
ddX[1]/=len;
ddX[2]/=len;
Как мы видим, я не забыл, что нам нужен именно единичный вектор (с длиной равной единице), поэтому я посчитал длину вектора от точки point к точке point2 и разделил каждую координату на длину. Эта процедура называется нормализация вектора – приведение его к единичной длине с сохранением направления.
Ну и ddY по старой схеме (как в пункте 1, где мы экран рисовали) определяем как векторное произведение ddX на ddZ:
ddY[0] = ddX[1]*ddZ[2] - ddX[2]*ddZ[1];
ddY[1] = ddX[2]*ddZ[0] - ddX[0]*ddZ[2];
ddY[2] = ddX[0]*ddZ[1] - ddX[1]*ddZ[0];
Таким образом, мы можем задать все 6 плоскостей. Например, плоскость, ограничивающая параллелепипед «снизу» определяется так:
spoint[0] = point[0] - z * ddZ[0];
spoint[1] = point[1] - z * ddZ[1];
spoint[2] = point[2] - z * ddZ[2];
n[0] = -ddZ[0];
n[1] = -ddZ[1];
n[2] = -ddZ[2];
где point — нулевая точка нашей поверхности, а z - половина высоты параллелепипеда.
Остальные – по аналогии, меняем только - на + и буквы координат.
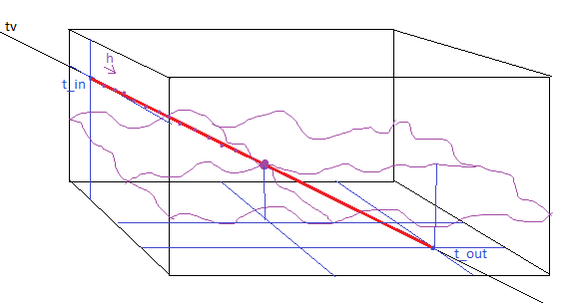
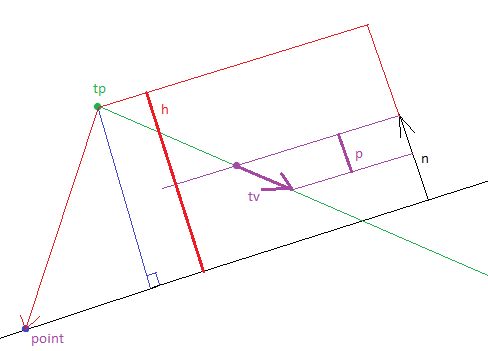
Дальше нужно в общем виде понимать, как мы будем искать точки пересечения луча и плоскости. Допустим, плоскость задана точкой point[3] и нормалью n[3]. Луч задан точкой tp[3] и вектором tv[3]. Еще одна картинка в стиле «я у мамы paint master»:
Несложно догадаться, что если векторы n и tv имеют единичную длину, то расстояние от точки tp до точки пересечения с плоскостью будет равно -h/p. Шучу, сложно догадаться. Но при желании вы можете это проверить. Даже так – если вы сейчас в школе проходите векторную алгебру – вы должны это проверить и выложить в комментариях доказательство. Иначе вам поставят двойку. Или что там сейчас ставят в школах…
Как же найти эти h и p? Тут на помощь снова приходят определения из векторной алгебры. Скалярное произведение векторов численно равно длине проекции одного из этих векторов на другой. Как определить скалярное произведение? А примерно так:
float MulVecSc(float *Vec1, float *Vec2){
return Vec1[0]*Vec2[0] + Vec1[1]*Vec2[1] + Vec1[2]*Vec2[2];
};
Как мы видим из рисунка, h – это проекция на нормаль вектора от точки tp до точки point, принадлежащей плоскости, а p – это проекция на нормаль вектора tv.
vp[0] = point[0] - tp[0];
vp[1] = point[1] - tp[1];
vp[2] = point[2] - tp[2];
p = MulVecSc(n,tv);
h = MulVecSc(n,vp);
t = - h/p;
Знак p покажет нам, с какой стороны плоскости мы находимся (а значит покажет, нашли мы точку «входа» или «выхода»).
Резюмируем. В пространстве точки пересечения луча с параллелепипедом находятся так:
float ddY[3] = {point2[0],point2[1],point2[2]};
float ddX[3] = {0,0,0};
float ddZ[3] = {n[0],n[1],n[2]};
tmMulVec(n,ddY,ddX);
// 6 плоскостей. Ищем самый поздний "вход" и самый ранний "выход"
// Плоскость 1
spoint[0] = point[0] + x * ddX[0];
spoint[1] = point[1] + x * ddX[1];
spoint[2] = point[2] + x * ddX[2];
vp[0] = tp[0]-spoint[0];
vp[1] = tp[1]-spoint[1];
vp[2] = tp[2]-spoint[2];
n[0] = ddX[0];
n[1] = ddX[1];
n[2] = ddX[2];
p = tmMulVecSc(lv_n,tv);
t = - tmMulVecSc(lv_n,lv_vp)/p;
if(p>0.0f){ // выход
if(t<t_out)
t_out = t;
}else{ // вход
if(t>t_in)
t_in = t;
};
// Плоскость 2
spoint[0] = point[0] - x * ddX[0];
spoint[1] = point[1] - x * ddX[1];
spoint[2] = point[2] - x * ddX[2];
vp[0] = tp[0]-spoint[0];
vp[1] = tp[1]-spoint[1];
vp[2] = tp[2]-spoint[2];
n[0] = -ddX[0];
n[1] = -ddX[1];
n[2] = -ddX[2];
p = tmMulVecSc(lv_n,tv);
t = - tmMulVecSc(lv_n,lv_vp)/p;
if(p>0.0f){ // выход
if(t<t_out)
t_out = t;
}else{ // вход
if(t>t_in)
t_in = t;
};
// Плоскость 3
// ...
// Плоскость 4
// …
// Плоскость 5
// …
// Плоскость 6
// ...
if(t_in<t_out&&t_out>0){
// есть пересечение
};
Так. Теперь мы знаем, что в промежутке от t_in до t_out мы внутри параллелепипеда.
Дальше, как и планировали, будем проверять каждую точку с неким шагом h на то, находится она выше или ниже поверхности в локальных координатах.
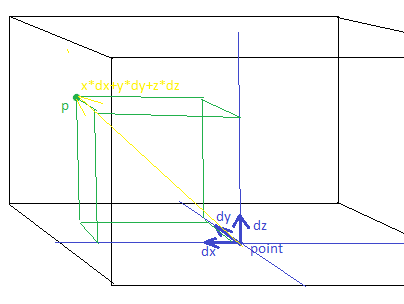
Что такое локальные координаты?
Это система координат, образованная теми самыми ddX, ddY, ddZ которые мы определили выше. Как очевидно из рисунка (на этот раз действительно очевидно), если у нас есть точка p, то вектор, ведущий от нулевой точки нашей поверхности до точки p будет определяться векторной суммой x*ddX+y*ddY+z*ddZ, где x y и z локальные координаты этой точки. Что ж, в таком случае, зная глобальные координаты точки p мы можем получить локальные таким образом:
vtp[0] = p[0]-point[0];
vtp[1] = p[1]-point[1];
vtp[2] = p[2]-point[2];
x = MulVecSc(ddX,vtp);
y = MulVecSc(ddY,vtp);
z = MulVecSc(ddZ,vtp);
Дальше, проверяем, находимся мы в этой точке под поверхностью или над.
F = F_xy; // тут у нас определение значения функции, описывающей плоскость. Его мы рассмотрим позже, в 3й части.
if(z<F){ // определяем, находимся мы в точке входа «над» или «под» поверхностью
in = true;
}else{
in = false;
};
Дальше – просто делаем это в цикле, перемещая точку p:
for(t = t_in+h;t<=t_out;t+=h){
pt[0] = tp[0] + tv[0]*t;
pt[1] = tp[1] + tv[1]*t;
pt[2] = tp[2] + tv[2]*t;
vtp[0] = point[0]-pt[0];
vtp[1] = point[1]-pt[1];
vtp[2] = point[2]-pt[2];
x = -tmMulVecSc(ddX,vtp);
y = -tmMulVecSc(ddY,vtp);
z = -tmMulVecSc(ddZ,vtp);
F = F_xy;
if(z<F){ // сейчас внутри
if(!in){ // были снаружи
break;
};// были снаружи
}else{ // сейчас снаружи
if(in){ //были внутри
break;
};//были внутри
}; // внутри/снаружи
}; // for t_in ... t_out
if(t>=t_out){
break; // никакого пересечения не было
};
// на данный момент t – это расстояние от точки tp до точки пересечения
// фактически точка на расстоянии t уже после пересечения с плоскостью, поэтому
// в качестве точки пересечения берем t-h
t-=h
collision_pt[0] = tp[0] + tv[0]*t;
collision_pt[1] = tp[1] + tv[1]*t;
collision_pt[2] = tp[2] + tv[2]*t;
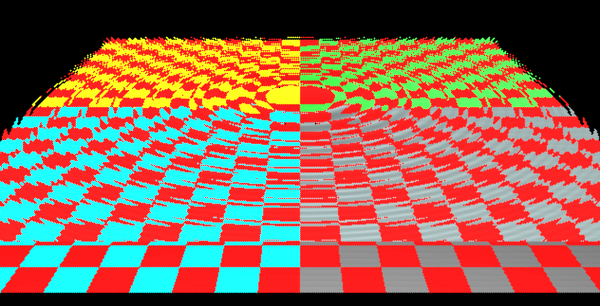
Вот мы и нашли, где луч пересек поверхность. Запихнув это решение в цикл, который мы получили в первой части, мы получим картинку, на которой будут видны очертания поверхности. Но на 3d картинку это не будет похоже – чтобы одна точка поверхности отличалась от другой (что создаст объем) нужно определить освещенность.
3. Определение освещенности точки.
В рамках этой задачи мы не будем заморачиваться с источниками света – будем считать, что у нас один источник и он расположен непосредственно за «глазом». В таком случае расчет освещенности сводится к простому определению нормали к поверхности. Чем меньше значение проекции – тем темнее точка, так как свет падает под большим углом. Поскольку векторы у нас единичные, значение проекции будет изменяться в диапазоне [0..1], что позволяет просто домножать значение цвета на проекцию и получать нужную картинку.
Итак, вернемся к «простому определению нормали».
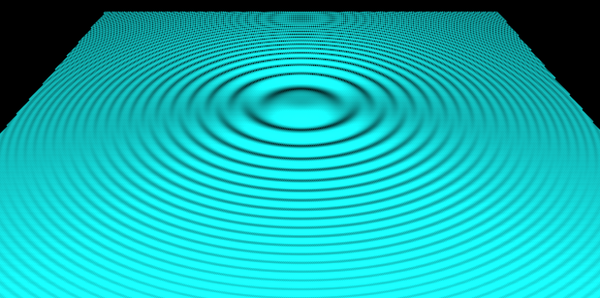
Пора наконец определиться с тем, какую поверхность мы рисуем. В коде ранее была конструкция F = F_x; Тут F_x это макрос, в который я подставляю формулу, которую хочу рисовать. Разумеется, в последствии в код можно будет подставить любую формулу, но для примера нужно взять что-то конкретное. Я выбрал такое:
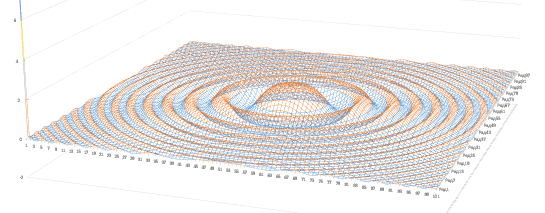
#define F_xy cos((x*x+y*y)/20.0)/(1+(x*x+y*y)/100.0)
Чтобы понимать, что мы хотим увидеть в программе, построим этот график в каком-нибудь инструменте, который это уже умеет:
Так как же определить нормаль в какой-нибудь точке поверхности? Нормаль – это вектор перпендикулярный касательной плоскости к поверхности в заданной точке, правильно? А коэффициент угла наклона касательной к графику функции в точке – это ни что иное как производная функции в этой точке. Таким образом, нужно просто взять с обратным знаком производные исходной функции по трем координатам – это и будет вектор нормали.
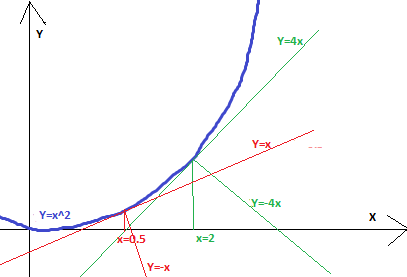
Для примера возьмем двумерный график:
(графики касательных смещены для наглядности)
Функция Y=x^2. Её производная Y'=2x. Соответственно, в точке X=0.5 коэффициент угла наклона равен единице, а в точке 2 – четырем. Из графика видно, что коэффициент угла наклона с обратным знаком показывает угол наклона линии, перпендикулярной касательной. Эта же логика работает и для более сложных графиков. Так же она работает и в пространстве.
Поэтому запишем уравнение поверхности в виде cos((x*x+y*y)/20.0)/(1+(x*x+y*y)/100.0) - z = 0 и возьмем производные по трем координатам:
F'x = ((sin((x*x+y*y)/20.0)*x/10.0)*(1+(x*x+y*y)/100.0)-(x/50.0)*cos((x*x+y*y)/20.0))/((1+(x*x+y*y)/100.0)*(1+(x*x+y*y)/100.0))
F'y = ((sin((x*x+y*y)/20.0)*y/10.0)*(1+(x*x+y*y)/100.0)-(y/50.0)*cos((x*x+y*y)/20.0))/((1+(x*x+y*y)/100.0)*(1+(x*x+y*y)/100.0))
F'z = -1
Вернемся к коду. Теперь зная точку пересечения и ее локальные координаты – мы можем найти нормаль. Она будет определяться как N[3] = {-F'x,-F'y,-F'z}. Но нужно помнить, что это ее значения в локальных координатах. Чтобы перевести в глобальные – нужно каждый компонент умножить на значение вектора той оси, которой он соответствует:
#define F_x ((sin((x*x+y*y)/20.0)*x/10.0)*(1+(x*x+y*y)/100.0)-(x/50.0)*cos((x*x+y*y)/20.0))/((1+(x*x+y*y)/100.0)*(1+(x*x+y*y)/100.0))
#define F_y ((sin((x*x+y*y)/20.0)*y/10.0)*(1+(x*x+y*y)/100.0)-(y/50.0)*cos((x*x+y*y)/20.0))/((1+(x*x+y*y)/100.0)*(1+(x*x+y*y)/100.0))
#define F_z 1.0
float Fx = F_x;
float Fy = F_y;
float Fz = F_z;
collision_normal[0] = ddX[0]*Fx+ddY[0]*Fy+ddZ[0]*Fz;
collision_normal[1] = ddX[1]*Fx+ddY[1]*Fy+ddZ[1]*Fz;
collision_normal[2] = ddX[2]*Fx+ddY[2]*Fy+ddZ[2]*Fz;
Теперь мы готовы определять компоненты цвета в заданной точке. Допустим, базовый цвет поверхности у нас лежит в переменной rgb:
Shade = 255.0f * MulVecSc(collision_normal,tv);
if(Shade < 0)
Shade = -Shade;
r = Shade * rgb[0];
g = Shade * rgb[1];
b = Shade * rgb[2];
Оценим результат:
Сменим формулы:
#define F_xy 0.3*(sin(x)*cos(y/2.0)+cos(x/2.5)*sin(y/1.5))
#define F_x -0.3*(cos(x)*cos(y/2.0)-sin(x/2.5)*sin(y/1.5))
#define F_y -0.3*(-sin(x)*sin(y/2.0)+cos(x/2.5)*cos(y/1.5))
Если кого-нибудь заинтересовало – подписывайтесь. Если будет достаточно желающих – освещу другие моменты и задачи, с которыми я столкнулся в ходе разработки: преломление, рассеивание света. Картинка для затравки (на ней чуть менее чем всё, что сейчас умеет программка, в ходе реализации которой я столкнулся с описанной выше задачей):